https://www.acmicpc.net/problem/1011
1011번: Fly me to the Alpha Centauri
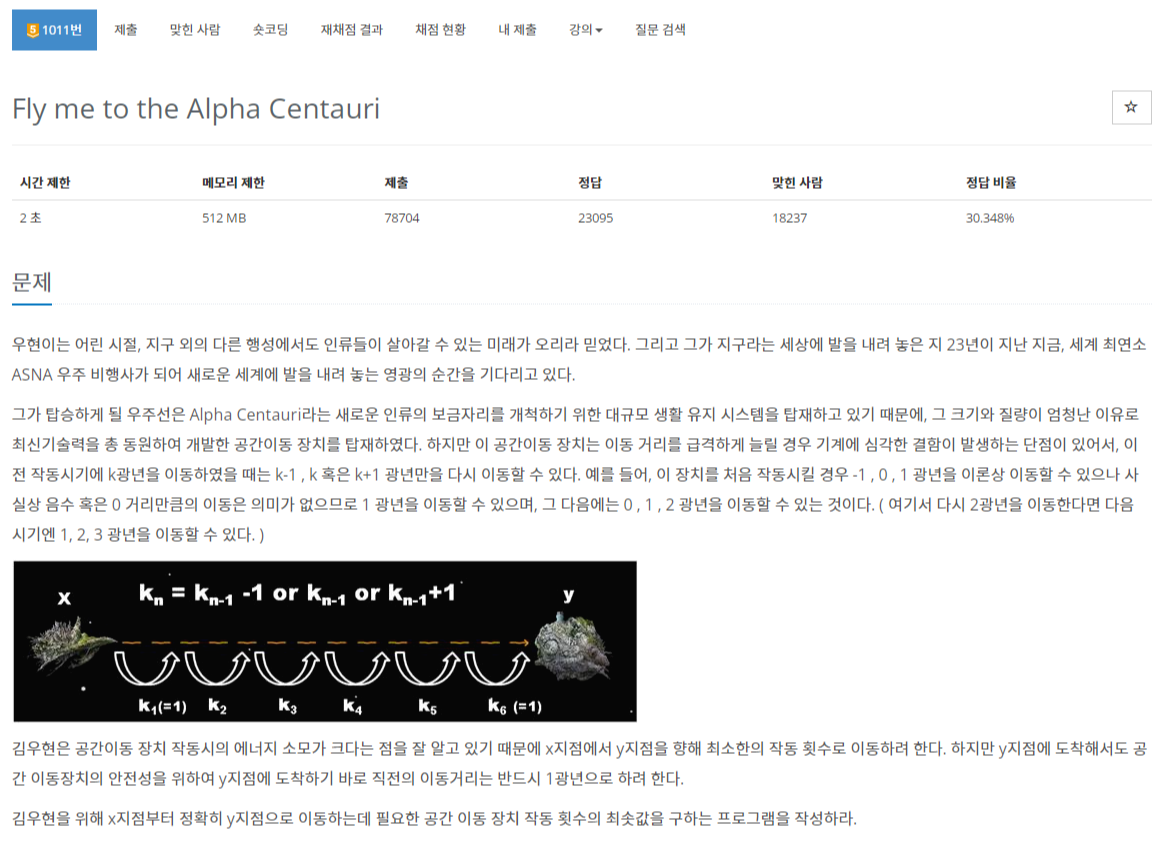
우현이는 어린 시절, 지구 외의 다른 행성에서도 인류들이 살아갈 수 있는 미래가 오리라 믿었다. 그리고 그가 지구라는 세상에 발을 내려 놓은 지 23년이 지난 지금, 세계 최연소 ASNA 우주 비행
www.acmicpc.net
https://dev-minji.tistory.com/52
[백준/C++] 1011번 : Fly me to the Alpha Centauri
문제 우현이는 어린 시절, 지구 외의 다른 행성에서도 인류들이 살아갈 수 있는 미래가 오리라 믿었다. 그리고 그가 지구라는 세상에 발을 내려 놓은 지 23년이 지난 지금, 세계 최연소 ASNA 우주
dev-minji.tistory.com
설명이 어려워 위의 블로그에서 풀이를 가져 왔다.
풀이
이 문제는 규칙을 정확하게 찾아야 해서 조금 어려웠다. 총 2가지의 규칙이 있는데 첫 번째 규칙까지만 알아내서 다른 블로그를 참고하여 코드를 짰다.
01. 처음과 마지막에는 무조건 1광년을 이동해야 한다.
문제의 핵심은 "마지막에 1광년을 이동해야 한다"는 것이다.
때문에 이동할 경우 1 -> 2 -> .... -> 2 -> 1 순서로 이동해야 한다.
1 > 2 > 1 = 1+2+1 = 4 -> 2*2 (이동횟수 3)
1 > 2 > 3 > 2 > 1 = 1+2+3+2+1 = 9 -> 3*3 (이동횟수 5)
1 > 2 > 3 > 4 > 3 > 2 > 1 = 1+2+3+4+3+2+1 = 16 = 4*4 (이동횟수 7)
=> 최대 이동 속도 = N^2, 이동 횟수 = 2N-1임을 확인할 수 있다.
02. 차원 이동의 횟수 계산
위의 계산으로 두 지점 간의 거리가 제곱수일때의 최소 이동 횟수를 구했다. 다른 경우에는 어떨까?
https://jaynamm.tistory.com/entry/%EB%B0%B1%EC%A4%80-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-1011%EB%B2%88-Fly-me-to-the-Alpha-Centauri 님이 올린 표에 잘 정리되어 있다.
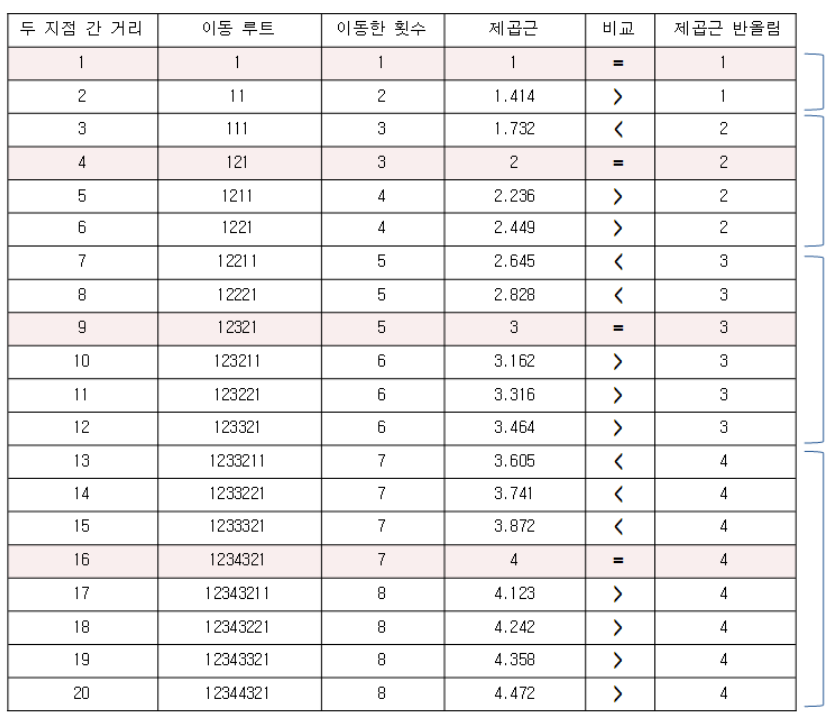
각 거리의 제곱근과 제곱근의 반올림 값을 보면
제곱근 <= 반올림값일 경우, 2*반올림 - 1
제곱근 > 반올림값일 경우 2*반올림
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
using System;
using System.Text;
class Program{
static int Cal(int start, int end){
int distance=end-start;
double N = Math.Sqrt(distance);
//N을 반올림하고 나서 (int)로 변환해줘야함. 하지않으면 반올림되서 정수형태지만 double로
//인식되서 타입오류뜸.
int Nround = (int)Math.Round(N);
if(N<=Nround){
return Nround*2-1;
}else{
return Nround*2;
}
}
static void Main(){
StringBuilder sb = new StringBuilder();
int t = int.Parse(Console.ReadLine());
for(int i=0;i<t;i++){
string[] s = Console.ReadLine().Split();
int start=int.Parse(s[0]);
int end=int.Parse(s[1]);
sb.Append(Cal(start, end)+"\n");
}
Console.WriteLine(sb);
}
}
|
cs |
Sqrt를 이용해 제곱수를 구하고, 구한 제곱수를 Round를 이용해 반올림해 제곱수와 반올림한 값을 비교함.
'C# > 백준 알고리즘' 카테고리의 다른 글
| 2022.01.26 [백준] C# 네 번째 점 (0) | 2022.01.26 |
|---|---|
| 2022.01.26 [백준] C# 직사각형에서 탈출 (0) | 2022.01.26 |
| 2022.01.25 [백준] C# 부녀회장이 될테야 (0) | 2022.01.25 |
| 2022.01.25 [백준] C# ACM호텔 (0) | 2022.01.25 |
| 2022.01.25 [백준] C# 큰 수 A+B (0) | 2022.01.25 |




댓글