728x90
반응형
https://www.acmicpc.net/problem/9020
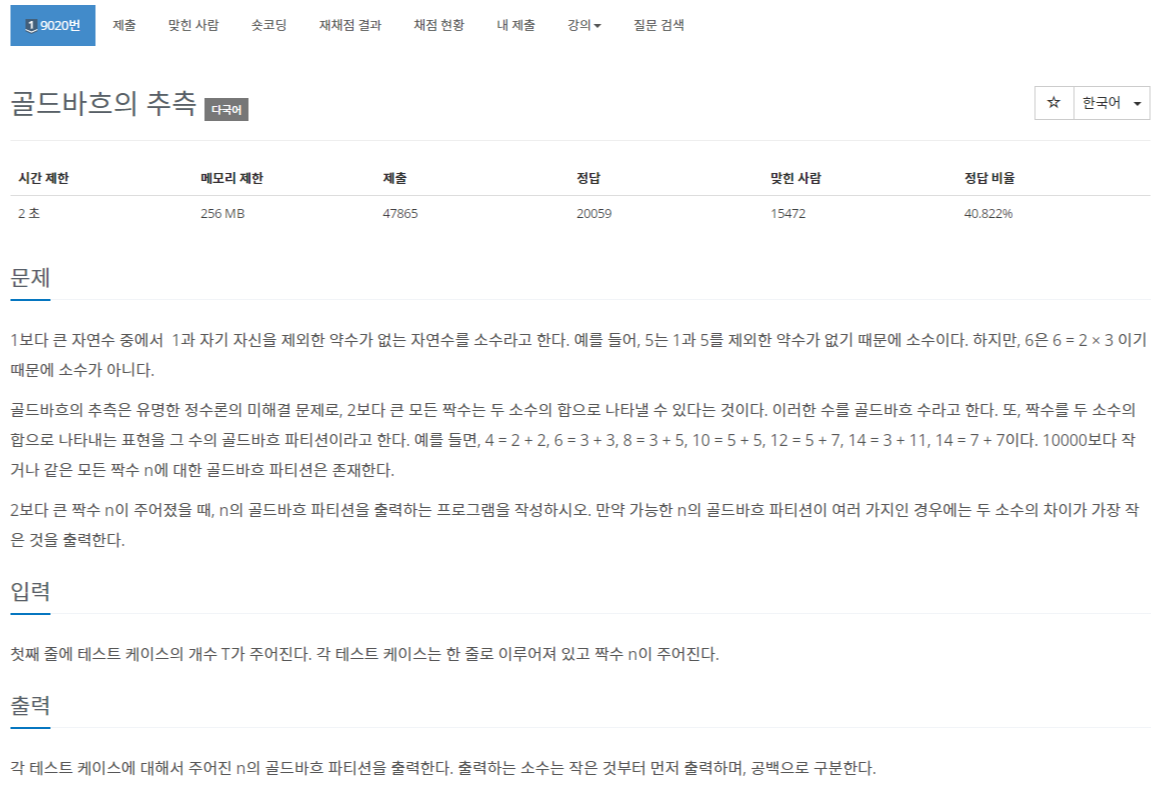
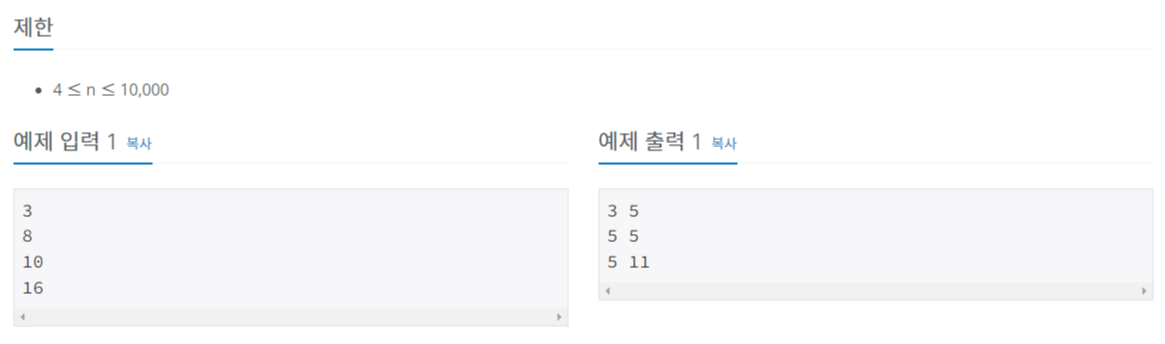
9020번: 골드바흐의 추측
1보다 큰 자연수 중에서 1과 자기 자신을 제외한 약수가 없는 자연수를 소수라고 한다. 예를 들어, 5는 1과 5를 제외한 약수가 없기 때문에 소수이다. 하지만, 6은 6 = 2 × 3 이기 때문에 소수가 아
www.acmicpc.net
풀이
-시간초과 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Diagnostics;
using System.Threading;
namespace ConsoleApp1
{
class Program
{
//길이가 a만큼되는 bool배열을 만든다.
//배열 중에서 소수가 아닌 값들은 true로 선언.
//더해서 a가 되는 값을 찾고 그 중, 두 수 모두 소수인 값을 찾는다.
//소수인 값들 중, 차이가 가장 적은 쌍을 찾는다.
//차이가 가장 적은 쌍중 작은 값을 return한다.
static int Goldbach(int a)
{
if (a == 4)
{
return 2;
}
//bool배열을 선언하면 처음 각 요소는 false값을 가진다.
bool[] check = new bool[a];
check[0] = true;
check[1] = true;
for (int i = 2; i < a; i++)
{
for(int j = 2; j < i; j++)
{
if (i % j == 0 && j!= i)
{
check[i] = true;
break;
}
}
}
int sosu_Sub = a;
int minSosu = 0;
for (int i = 2; i <= a / 2/+1; i++)
{
for(int j = i; j < a; j++)
{
if (i + j == a && check[i] == false && check[j] == false)
{
if (j - i < sosu_Sub)
{
minSosu = i;
}
}
}
}
return (minSosu);
}
static void Main()
{
Stopwatch sw = new Stopwatch();
sw.Start();
StringBuilder sb = new StringBuilder();
int n = int.Parse(Console.ReadLine());
for (int i = 0; i < n; i++)
{
int a = int.Parse(Console.ReadLine());
int x = Goldbach(a);
sb.Append(x + " " + (a - x) + "\n");
}
Console.WriteLine(sb);
sw.Stop();
Console.WriteLine(sw.Elapsed);
}
}
}
|
cs |
위의 방식으로 코드를 짜서 콘솔창에선 정답으로 나오지만 시간을 측정한 결과 4초가 조금 넘는 시간이 걸려 시간초과가 나왔다.
-정답 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
using System;
using System.Text;
class Program{
static void Main(){
StringBuilder sb = new StringBuilder();
bool[] check = new bool[10001];
for(int i = 2; i < 10001; i++)
{
if (check[i] == false)
{
/* 에라토스테네스의 체에 맞게 소수를 구함
만일, check[i]가 false이면 i 이후의 i 배수는 약수로 i를
가지고 있는 것이 되므로 i 이후의 i 배수에 대해 true값을 준다.
check[i]가 true이면 i는 이미 소수가 아니므로 i의 배수 역시
소수가 아니게 된다. 그러므로 검사할 필요도 없다.
*/
for (int j = i * i; j < 10001; j += i)
{
check[j] = true;
}
}
}
int n = int.Parse(Console.ReadLine());
for (int i = 0; i < n; i++)
{
int a = int.Parse(Console.ReadLine());
//소수의 합이 a가 되면서 차이가 가장 적은 쌍을 찾기 위해
//a의 절반 값에서 시작
//조건에서 a는 짝수라고 했기 때문에 /2 를해도 절반이 됨.
int x = a / 2;
int y = a / 2;
while (true)
{
if (check[x] == false && check[y] == false)
{
sb.Append(y + " " + x + "\n");
break;
}
else
{
//x는 증가시키고 y는 감소시키면서 찾음.
x++;
y--;
}
}
}
Console.WriteLine(sb);
}
}
|
cs |
위의 코드는 에라토스테네스의 체를 사용하여 코드를 작성했다. 에라토스테네스의 체를 사용하니 코드도 훨씬 줄어들고 처리 시간도 절반정도 줄어들었다.
728x90
반응형
'C# > 백준 알고리즘' 카테고리의 다른 글
| 2022.01.28 [백준] C# 피보나치 수 5 (0) | 2022.01.28 |
|---|---|
| 2022.01.28 [백준] C# 팩토리얼 (0) | 2022.01.28 |
| 2022.01.27 [백준] C# 베르트랑 공준 (0) | 2022.01.27 |
| 2022.01.27 [백준] C# 터렛 (0) | 2022.01.27 |
| 2022.01.27 [백준] C# 소인수분해 (0) | 2022.01.27 |




댓글